ささいな疑問
定木(定規)とコンパスによる作図問題でふと思いついた。
(1)長さを\(n\)倍、ないし\(n\)等分することは当該線分を与えられるだけで可能。
(2)ある正方形の\(n\)倍の面積を持つ正方形の作図は当該正方形を与えるだけで可能。
いずれも「単位長さ」は必要ない(どう定めようと結果はかわらない)。
ここで、
ある長さの平方根をもつ長さは、当該線分が与えられただけでは作図できない。
単位長さ1の線分が別に必要である(単位長さの定め方によって結果がかわる)。これはなぜか(どのように説明するか)?
実は10年ほど前に「教えて!goo」に質問してみた。9件ほどの回答があったが、結局のところ釈然としなかった。
この「現象」を戯画的に描いてくれた回答に FT56F001さんによるコメントがあり、次のようなものである。きわめてわかりやすく説明してくれるので、そのまま引用する。
この線分の長さの平方根を持つ線分を作図せよ,と言われました。
元の線分を物差しで測ると10cmの長さでした。
√10=3.16なので3.16cmの線分を作図したところ,間違いだと言われました。
元の線分は100mmの長さなので,10mmの線分を作図するんだよ。
1cmの線分を作図したところ,間違いだと言われました。
元の線分は0.1mの長さなので,0.316mの線分を作図するのね。
31.6cmの線分を作図したところ,間違いだと言われました。
元の線分は10/2.54=3.93inchの長さをもっています。あなたは長さ1.98inchの線分を描くべきだったのです。
5.03cmの線分を作図したところ,間違いだと言われました。
元の線分は10/3.03=3.3寸の長さやし,1.82寸=5.5cmの線分を描かなあかんで。
(No.8 回答者: FT56F001 回答日時:2011/10/24 11:53)
簡潔な答えはこれより前にでているbanakonaさんの回答で「これは、質問者さん自身が言っている「単位長さの定め方によって結果がかわる」からに尽きるんじゃないでしょうか。同じ理由で、単位長さが必要な作図に「与えられた長さの逆数」の作図があります。」とある。実はまったくつまらない問題という気もしてくる。
一方、同じbanakonaさんの回答に「与えられた2本の線分a,bの相乗平均の作図は、√(ab)であるにも拘らず単位長さが不要」というのは興味をひく。
改めて考えてみると、\(a,b,c\)を具体的線分で与えるとして
単位長なしでできる作図の例
$$ \sqrt{ab} ,\frac{ab}{c} $$
単位長が必要な作図の事例
$$ \sqrt{a} , \frac{1}{a}, ab, \frac{b}{a}, a^2$$
この違いはどこに生じるのだろうか?
実は「教えて!goo」では、具体的な作図方法は示さなかった。そこで、まずそれを示すことにする。
与えられた長さの平方根の作図
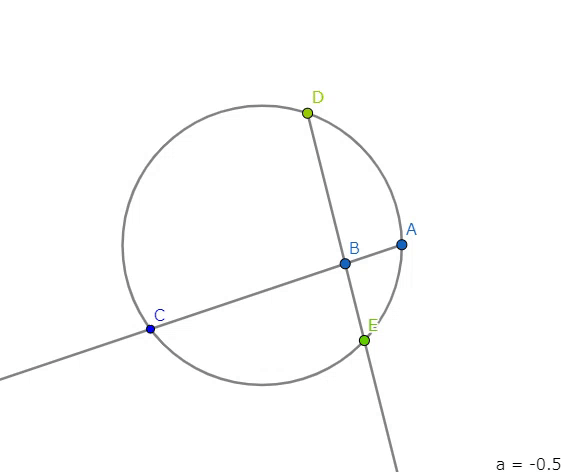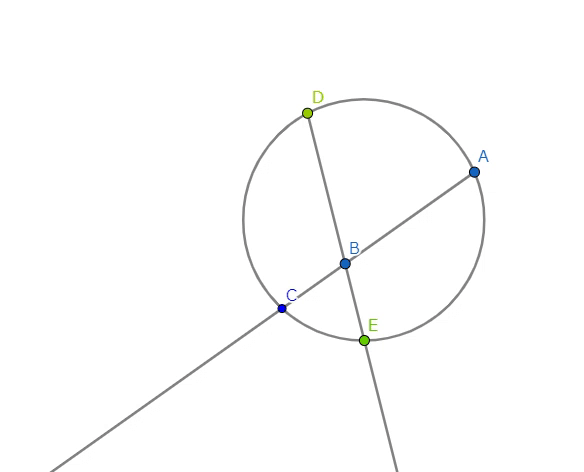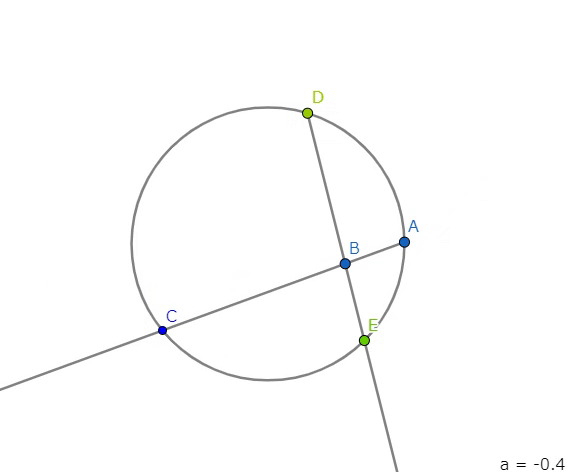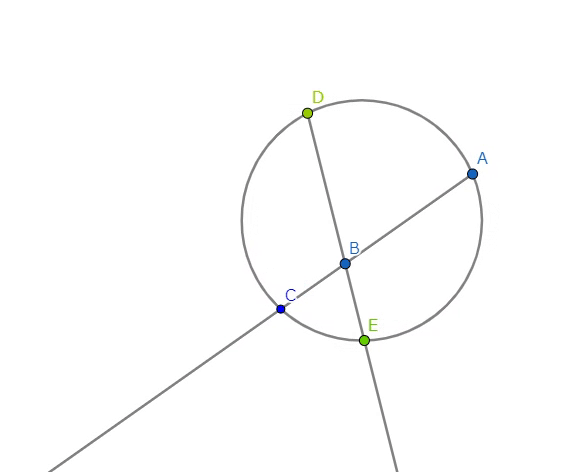
いま、与えられた直線の長さ\(x\)を\(BC\)にとり、その直線の延長上に\(AB\)が単位長となるように点\(A\)をとる。
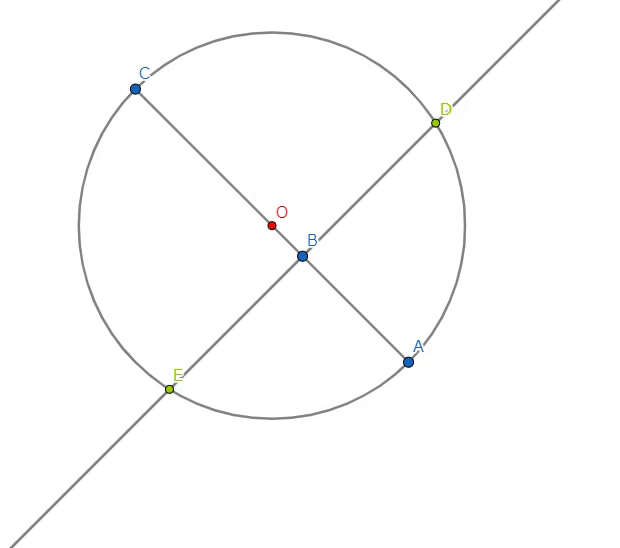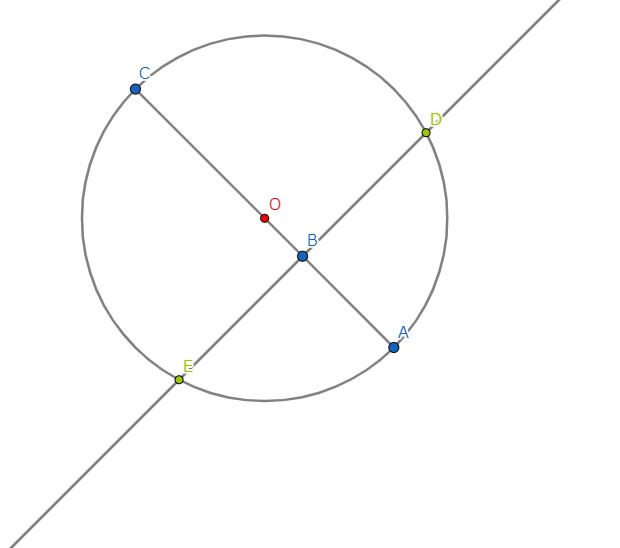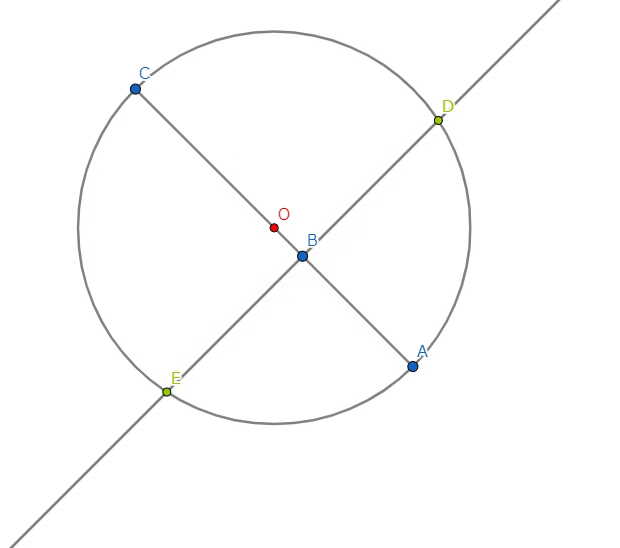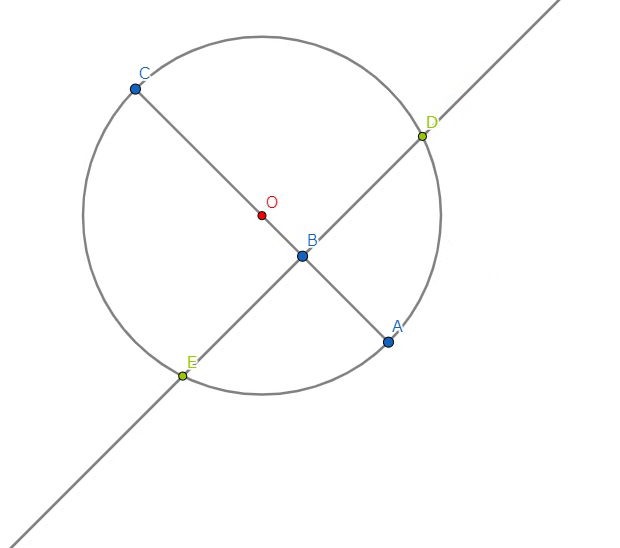
\(AC\)を直径とする円を描く。\(B\)を通る垂線を引き、円との交点をそれぞれ\(D,E\)とする。
\(AB*BC=DB*BE\) が成立する(方べきの定理)。
$$ DB=BE, BC=x, AB=1$$
$$ DB^2 = x*1, DB = \sqrt{x}$$
つまり\(BD\)が求める長さとなる。上記アニメーションにより単位長\(AB\)が変化すると、\(BD\)も変化する。すなわち与えられた線分だけでは「その平方根の長さを持つ線分」は作図できず、別に単位長が必要である。上記の作図によれば、単位長をもつ具体的な線分は必要だが、もとの線分の長さを数値として知る必要はない。
【2つの長さの積の平方根の作図】
同じ図で説明可能(アニメーションをとめてみる)だが、2つの線分が具体的に与えられたとき、その長さの積の平方根の長さを持つ線分は、単位長が与えられなくとも作図可能である。
すなわち\(AB,BC\)にそれぞれの長さをとれば、\(DB\)の長さは\(AB,BC\)の長さの積の平方根となる。上記の円は固定され、この場合、単位長は必要ない(単位長をどう与えようが、線分\(DB\)は変わらない)。
2つの長さの積の長さ
2つの線分が具体的に与えられている。その積の長さは、それだけで作図できるか。この場合も単位長が与えられないと作図できない。手順は以下の通り。
コンパスでそれらの長さを一直線上、\(DB,BE\)にとる。
点\(A\)を\(AB\)が単位長となるようにとる。
三点\(D,AE\)を直径とする円を描く。直線\(AB\)の延長と円周の交点を\(C\)とする。
\(AB*BC=DB*BE\) が成立する(方べきの定理)。
$$ AB=1$$
$$ BC = DB * BE$$
やはり単位長のとり方によって変化する。
【2つの長さの積/一つの長さの作図:\(\frac{ab}{c}\)】
アニメーションをとめて考えれば\(DB, BE, AB\)の3つの長さを与えれば、
$$ \frac{ab}{c} $$
が決まる。この場合、単位長はいらない。
作図法の整理 いずれも方べきの定理
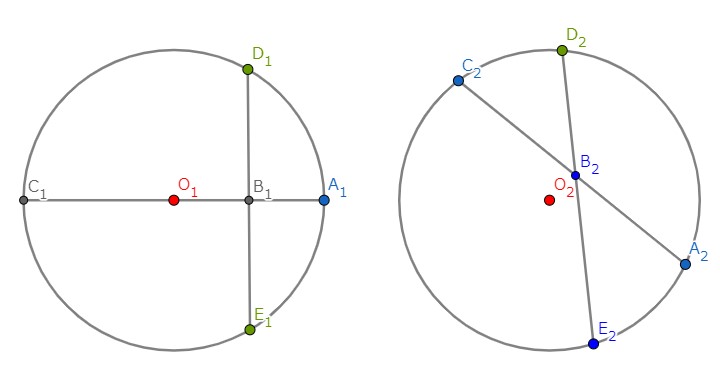
このように最初にあげた一連の問題は、方べきの定理を使うことが手がかりとなる。
$$AB*BC=DB*BE$$
左図の場合、特に\(A_1C_1\)は直径であり\(D_1E_1\)と直交、したがって、\(D_1B_1 = B_1E_1\)となっている。
左図の場合
\(D_1B_1 = B_1E_1=a , A_1B_1 = 1\)とすれば、\(B_1C_1 = a^2\) → 単位長が必要
\(D_1B_1 = B_1E_1=1 , A_1B_1 = a\)とすれば、\(B_1C_1 = \frac{1}{a}\) → 単位長が必要
(以下、既出)
\(B_1C_1 = a , A_1B_1 = 1\)とすれば、\(D_1B_1 = B_1E_1=\sqrt{a}\) → 単位長が必要
\(B_1C_1 = a , A_1B_1 = b\)とすれば、\(D_1B_1 = B_1E_1=\sqrt{ab}\) → 単位長が不要
右図の場合
\(D_2B_2 = a, B_2E_2=1 , A_2B_2 = b\)とすれば、\(B_2C_2 = \frac{a}{b}\) → 単位長が必要
(以下、既出)
\(D_2B_2 = a , B_2E_2= b , A_2B_2 = 1\)とすれば、\(B_2C_2 = ab\) → 単位長が必要
\(D_2B_2 = a , B_2E_2= b , A_2B_2 = c\)とすれば、\(B_2C_2 = \frac{ab}{c}\) → 単位長が不要
以上で最初の7つの長さの作図法を示した。この件に関し、単位長の必要性の有無についてはこれで完全に決定されたといえる。というのは、上記結果と逆の結果をもたらす手順があるとすると、それは方べきの定理と矛盾してしまうからである。
単位長が不要な場合の必要条件
さて、作図法を一応整理した以上までは、前置きに過ぎない。
線分\(l_1,l_2,・・・・,l_n\)が与えられている上で、線分\(D\)を作図できたとする。
これを2つの異なる単位系\(S_1,S_2\)で見てみる。
\(S_1\)系で見た長さを\(a_1,a_2,・・・・,a_n,d\)とし、
$$ d = f(a_1,a_2,・・・・,a_n)$$
との関係があるとする。
これを\(S_2\)系で見るとどうなるか。
\(S_2\)系で見た場合、それぞれの長さは、ある正の実数\(r\)を定数として\(ra_1,ra_2,・・・・,ra_n,rd\)となる。
この単位系でも先の関係が不変であるためには、
$$ rd = f(ra_1,ra_2,・・・・,ra_n)$$
となる必要があるので
$$ rf(a_1,a_2,・・・・,a_n)= f(ra_1,ra_2,・・・・,ra_n)$$
が成立する必要がある。これが単位長が不要な場合、すなわち単位長をどう定めようが関係が不変の場合の必要条件となる。
ちなみに、 \(\sqrt{ab} ,\frac{ab}{c}\)の場合、
$$ \sqrt{ra*rb} = r\sqrt{a*b} $$,
$$\frac{ra*rb}{rc} = r\frac{ab}{c} $$
となっており、単位長が不要の場合、必要条件を満たしている。
また、
$$\sqrt{(ra)^2+(rb)^2} = r\sqrt{a^2+b^2}$$
であり、条件を満たしているが言うまでもなくこの作図も単位長なしでできる(三平方の定理)。
先述した「単位長が必要な作図」である\( \sqrt{a} , \frac{1}{a}, ab, \frac{b}{a}, a^2\)は、この条件を満たさない。
もちろん、これは必要条件であり、例えば
$$(abc)^{1/3}$$
はこの条件を満たすが、 \((abc)^{1/3}\)は、そもそも定木とコンパスで作図できない(3つの線分を与え、その積の3乗根を作図すること)。
まとめ
以上により「単位長が不要な場合の作図」の必要条件までは明らかになった。
ただし、作図問題を離れ、単位系の変換、すなわち座標変換の問題に「過ぎない」点は不満が残る。
しかし、同時に冒頭に表明したとおり、まったくつまらない問題設定なのでは、という気もする。線分の長さ、ないし点の位置の実数値を考えるという発想は、そもそも作図問題を座標に翻訳して考えることから生まれ、つまり当然ながら単位長が前提にされているということだ。そういう意味では、この問題設定はかなり「転倒した」問題設定と言える。
当初の「教えて!goo」の回答に次のようなものが出てきたのも理解し得る。
「ある長さの平方根を持つ長さ」という言葉自体,
次元の考え方からすると異常で,あってはならない問題設定です(FT56F001)。
そもそもの作図問題では、「線分の平方根」など考えようがない。
とはいえ、少なくとも必要条件を定式化したことは10年来の問題のひとつの解決であった。



