東京出版の月刊誌「高校への数学」は私が中学3年のとき創刊された。その内容にわくわくしたものだが、創刊号に「フランクリンの凧」という平面図形の問題が「小学生でも理解できるが大学生でも解けない」難問として取り上げられていた。大学時代にときどき友人に出してみたが(今のようなネット検索ができない時代)、解けた人はいなかった。ただ一人、留学生が解析的に解けたと言っていたが解答は見せてもらえなかった。未だに印象深い問題である。
問題は次の通り。
【問題】
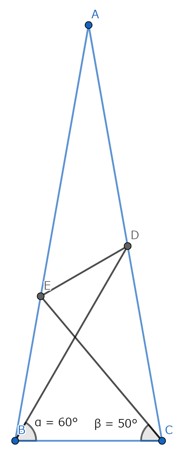
図1において
\(AB=AC,\angle A = 20^{\circ}\)
\(\angle DBC = 60^{\circ}\)
\(\angle ECB = 50^{\circ}\)
このとき、\(\angle BDE\)を求めよ。
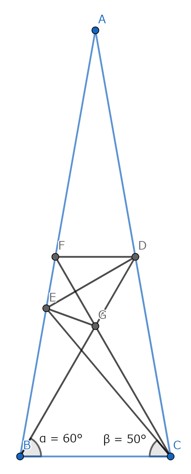
図2は解答にいたる補助線を引いた一例。
今でこそ「フランクリンの凧」と検索すれば、簡単にその内容は把握でき解法もでてくる。
もっとも多数の証明が紹介されているのは現代数学社によるもので14の解法がある。
うち証明例8が「フランクリンの凧」と呼ばれる証明であり、図2の解答例にあたる。フランクリンの凧とは四辺形EFDGのかたちがフランクリンが落雷実験であげた凧のかたちに似ているから、と冒頭の「高校への数学」の記事にあった。
一般的にはラングレー問題というそうだ。これもtsujimotterさんのノートブックに言及があった。



